이번주에 정리할 논문은 바로 GAN이다.
Generative Adversarial Network (GAN)
🔥등장 배경
지난 주 논문에서 등장한 모델인 VAE는 data likelihood를 maximization하기 위해서 여러가지 trick들을 이용했다. 원래 generator를 만들기 위해서 decoder를 붙여주고 완벽하게 최적화할 수 없는 부분은 버리고 Lower Bound를 optimization하는 방법을 활용했다.
→ 그러나 이렇게 푸는 것은 너무 복잡하다. 왜? VAE는 경험적으로 모델을 만든 것이 아니고, 수학적으로 증명을 시작해서 모델을 만든 것이기 때문. 즉 하려고 했던 것이 원래 모델의 density를 정확하게 모델링하고 싶었던 것
→ 근데 그렇게 하지말고 좀 더 practical하게 그냥 sampling을 했을 때 그림이 그럴듯하게 나오게만 만들면 안될까?
즉 GAN은 어떤 density function을 활용하지 않고, 대신에 game-theoretic을 이용한다 (어떤 2player가 게임을 하는 방식으로 distribution을 training 할 수있도록)
👉🏻 game-theoty란?
A라는 친구가 있고 B라는 친구가 있으면 서로의 decision을 알 수 있다(둘 다 분명하게 결정)
이때 A가 B의 결정을 보고 최적화하고 그 다음 B가 A의 최적화한 결과를 보고 본인의 결정을 다시 최적화하고, 그러면 또 A가 다시 B의 최적화된 결정을 보고 자신의 결정을 최적화하는 과정을 계속 반복
→ 그러다보면 결국에 equilibrium에 도달하게 된다(더 이상 더 나은 결정을 만들 수 없는 상태에 도달)
🔥 GAN의 구조

그럼 game-theory를 이용하기 위해서는 2 player가 있어야하는데, GAN에서 2 player는 누구인가?
Generator network와 Discriminator network
Generator : 가짜 사진을 만드는 네트워크
Discriminator : 진짜와 가짜를 구분할 수 있는 네트워크
→ 이 두가지 네트워크가 서로 경쟁하는 구조

이때 GAN의 구조를 살펴보면 앞에서 공부했던 AE나 VAE와 다르게 중간에 z가 있는 것이 아니고 일단 z부분으로 시작한다.
→ 즉 Encoder부분이 Discriminator부분이 되고, Decoder 부분이 Generator가 되는 그러한 구조이다.
<Generator랑 Discriminator가 하는 일>
- 따라서 Generator는 이미 압축된 저차원의 latent variable의 z가 Generator 네트워크를 통과하게 되면 이미지가 나오게 된다 → 복원이 되는 것!
- 그러면 방금 복원된 가짜이미지랑 진짜 우리가 가지고 있는 data set의 이미지인 x가 discriminator network로 들어간다. 이때 D(x)라는 것은 진짜 이미지가 들어간 것이고, D(G(z))는 만들어진 가짜 이미지가 들어간 것이다. 이때 이 Discriminator의 output이 1이면 real, 0이면 fake라고 예측을 한 것이다. 즉 discriminator가 정확하다면 D(x)는 항상 1이어야하고 D(G(z))는 항상 0이라고 답해야한다-> 그게 Discriminator 네트워크의 목적
- 그런데 !! Generator는 이 discriminator를 속이고 싶다!!
- (즉, 원래는 D(G(z))는 0이지만, 1이라고 답할 수 있도록 G(z)를 잘 만들어주려고 하는 것이 generator의 목적 ! → 즉 generator와 discrimination이 서로 경쟁한다)
🔥 Objective function/ loss function

따라서 objective function이 위와 같은 형태가 된다. 이 식은 Min Max problem이기 때문에 한번은 maximization문제를 풀고 동일한 V 함수에 대해서 한번은 minimization 문제를 푸는 서로 다른 두 개의 문제를 푼다 → 즉 한번은 generator를 위해서 한번은 discrimination을 위해서!
이제 좀 더 구체적으로 그게 무슨 말인지 살펴보자.
1. Discriminator 학습

일단 V를 먼저 maximization하게 된다.(V는 generator랑 Discriminator가 input으로 들어간 함수)
→ maximization을 할 때 max 밑에 있는 D가 Decision variable이고 이것을 내가 V를 maximization하는 방향으로 최적화 할 것이다.
→ 이때 최적화하는 것은 D이기 때문에 generator는 given이다(고정이다) = 학습된 generator를 갖다 쓰는 거고 그것을 가지고 나는 discriminator만 최적화한다!
그럼 이제 뒤의 식을 살펴보자!
<첫번째 항>
x가 data distribution을 따를 때(즉 진짜 데이터의 distribution에서 x를 가져오는 것) log(D(x))는 D(x)가 진짜 이미지가 들어왔을 때 이므로 discriminator가 잘 작동한다면 그 값이 1이 될 것이다(real이니까) 즉 D(x)가 0-1 사이의 값만 가질 수 있다는 것을 고려하면 log1은 전체값이 최대화된 것이라는 것을 알 수 있다.
<두번째 항>
z가 p(z)를 따를 때, 즉 latent space에서 z를 sampling하는 방법을 의미하기 때문에 가짜 이미지가 들어온 경우에 대한 식이다. 따라서 D(G(z))는 discriminator 입장에서는 0이 되어야할 것이다. 그러면 또다시 log1이 되기 때문에 전체 값이 최대화 된다.
→ 결국 여기서 하는 것은 Maximization인데, 오른쪽의 식을 최대화할 수 있는 것은 discriminator가 가짜를 0, 진짜를 1이라고 판별할 때이다!!
2. Generator 학습

이번에는 V를 Minimization하게 된다.
→ 이번에는 G를 최적화하는 것이기 때문에 D는 given이다. (앞에서 D를 최적화 했기 때문에 그 값을 가져와서 사용하면 된다.)
그럼 이제 뒤의 식을 살펴보자!
<첫번째 항>
원래 이 왼쪽 식에는 G가 들어있지 않다 → 즉 상수값으로 취급해서 학습에서 빠진다!
<두번째 항>
Generator 관점에서는 G(z)가 가짜이미지이지만, discriminator를 통과할 때 진짜처럼 보이기를 원한다. 따라서 G(z)가 1이 되고 오르쪽 항이 log0이 되면서 최소화 된다!
→ 이런 식으로 똑같은 V라는 함수를 discriminator는 최대화하지만, generator는 최소화하는 방향으로 학습한다.
👉🏻 Trick
그런데 generator를 학습할 때 한가지 trick을 사용할 수 있다.
먼저 log(1-x)와 log(x) 두 그래프를 생각해보자.
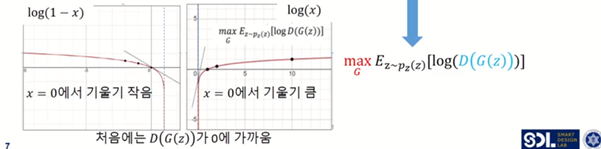
그래프는 전체적으로 y축 대칭이기때문에, log(1-x)를 minimize하는 것과 log(x)를 maximize하는 것을 사실 동일한 문제이다.
→ log(1-x)에서 minimize한다는 것은 그래프에서 오른쪽으로 가고싶다는 것
→ log(x)에서 maximize한다는 것은 그래프에서 오른쪽으로 가고싶다는 것
이때 x=0일때의 기울기를 한번 살펴보면, log(1-x)는 x=0일때 기울기가 완만한 반면, log(x)는 x=0일때 기울기가 굉장히 급하다. 즉, log(1-x)를 최적화하는 것보다 log(x)를 최적화하는 것이 더 용이하다고 해석할 수 있다. (기울기가 크다는 것은 그만큼 업데이트가 잘 된다는 것이기 때문에)
→ 따라서 log(1-D(G(z))을 최소화하는 것이 아니라 그냥 log(D(G(z))을 최대화하면 되는 것!!
→ 이제 가짜가 들어갔을 때 진짜다 라고 이야기해주면되니까 D(G(z))이 1이되면 되고, log1이 되기 때문에 최대화된다. 이렇게 trick을 이용해서 바꿔주면 generator가 조금 더 잘 학습할 수 있다.
→ 초반에는 당연히 discriminator가 더 학습이 쉽다. (새로운 데이터를 만드는 것보다 가짜/진짜를 구별하는 것이 더 쉽다) 따라서 처음에는 generator가 잘 작동을 안하기 때문에 아무리 generator가 G(z)를 열심히 만들어도 항상 D가 0에 가깝게 된다.(discriminator가 잘 안속고, 얘가 가짜라는 것을 금새 알아차림!!) = 즉 D(G(z))는 초깃값이 0이라는 뜻이기도 함. 그래서 trick을 이용!
따라서! 방금 살펴본 두가지 최적화를 너한번 나한번 너한번 나한번 반복하다보면 최종적으로 equilibrium에 도달한다
→ 즉 다시말해, 어느순간 discriminator가 들어온 데이터에 대해 이게 진짜인지, 가짜인지 판별을 하지 못하는 , 진짜가 들어오나 가까가 들어오나 output이 1/2이 나오는 상황이 될때까지 generator를 학습시키면 generator가 그때부터 굉장히 진짜와 유사한 디자인을 만들기 시작한다!!
여기서부터는 이 과정에 대한 증명과정을 다룰 것이다.
🔥 Proof
이제 그럼 증명 타임이다..!
Generative model의 목적을 다시 한번 떠올려보면, 내가 가지고 있는 data distribution과 가장 유사한 generator의 distribution을 만드는 것이였다.
즉! Pdata와 Pg의 거리가 최소화될 수 있도록 만들어주는 것이다
→ GAN은 이 문제를 V(D,G)를 mim, max 문제로 푼다. 이걸 generative model의 관점에서 보면 Pdata와 Pg가 동일한 distribution이면 즉, 그 거리가 최소화 되면 만족을 하는 것이다!
→ 여기서 jenson-shannon divergence를 쓰면, 두 식이 동일해지면 GAN theory로 푸는 것과 수학적으로 두 distribution이 같다고 푸는 것과 동일하다는 것을 증명할 수 있다!!
👉🏻 Discriminator 최적해 증명
(다 수식이라서 SLIDE 필기로 대체합니당)


👉🏻 Generator 최적해 증명

→ 따라서! GAN의 game theory로 풀었을 때 나오는 최종해가 기본적인 generator model의 컨셉과 동일하다는 것을 증명할 수 있다!!
🔥VAE vs GAN

마지막으로 VAE와 GAN을 비교한 그림이다.
→ 먼저 VAE로 만든 이미지는 Blurry하며, input이미지와 유사하다는 경향을 띈다. 그에 반해 GAN으로 만든 이미지는 Sharp하며 input 데이터에서 보지 못했던 새로운 이미지들을 만들어준다.
→ 또한 VAE는 모든 디자인 Space에서 smooth하게 학습하지만, GAN은 Mode collapse가 잘 발생한다. mode collapse란, 이미지가 잘나오는 곳에서만 잘나오고 이상한 곳에서 뽑으면 이상한 이미지가 나오는 것이다. 수학적으로 엄밀하게 학습하는 것이 아니라 generator가 속이기만 하면 되는 것이기 때문에, 잘만드는 것만 계속 잘 만들어내는 쪽으로 학습할 수 있다.
→ 또한 GAN은 game theory식으로 학습하면 convergence가 잘 일어나지 않고 발산할 수 있다.
→ 최종적으로 VAE는 차원축소용으로 많이 사용하고, 새로운 이미지를 만들어 낼 때는 GAN을 많이 사용한다.
이렇게 GAN에 대해 정리해보았는데, VAE를 공부하고 난 뒤여서 그런지 그래도 조금은,, 수월했다
아래에는 GAN을 정리하는데 참고한 자료이다.
이번에도 강의들을 많이 참고해서 작성해보았다.
<참고 자료>
-숙명여자대학교 기계시스템학부 강남우 교수님 3.4.GAN 강의 youtu.be/cd-kj1ysqOc
-나동빈님의 GAN: Generative Adversarial Networks (꼼꼼한 딥러닝 논문 리뷰와 코드 실습) 강의 youtu.be/AVvlDmhHgC4



