이번에는 LSGAN 논문에 사용된 핵심 아이디어와 원리에 대해 정리한 글이다.
기본 아이디어는 GAN에 있기 때문에 내용은 길지 않다.
LSGAN
등장배경: Cross-Entropy의 vanishing gradient problem
기존의 WGAN을 제외한 DCGAN이나 cGAN과 같은 모델들은 Discriminator의 손실함수로 binary cross-entropy를 사용해 min-max game문제를 해결한다.
먼저 기존의 Entropy식을 다시한번 살펴보면 다음과 같다.
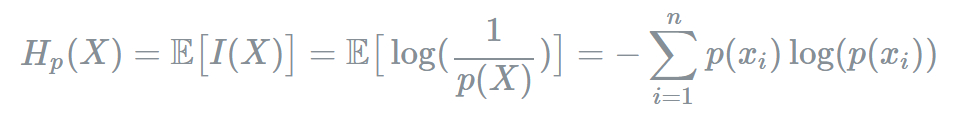
엔트로피는 정보량에 대한 기댓값이며 동시에 사건을 표현하기 위해 요구되는 최소 평균 자원이라고 할 수 있다.
(자세한 설명은 Entropy 글 참고)
따라서 위와 같은 식으로 나타낼 수 있다.
이어서 cross entropy는 true label에 대한 분포를 나타내는 true probability p와 현재 예측모델의 추정값에 대한 분포를 나타내는 q가 함께 등장해 다음과 같은 수식으로 표현된다.
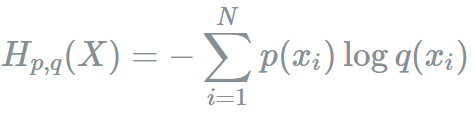
최종적으로 binary cross entropy란 두개의 class 중 하나를 예측하는 task에 대한 cross-entropy의 special case이며, 입력에 대한 신경망의 예측이 얼마나 진짜랑 유사한가를 통해 유사할 수 있도록 얼만큼 조정하면 되는지 이야기 해주는 loss라고 해석할 수 있다. 수식을 유도하는 과정은 아래와 같다.
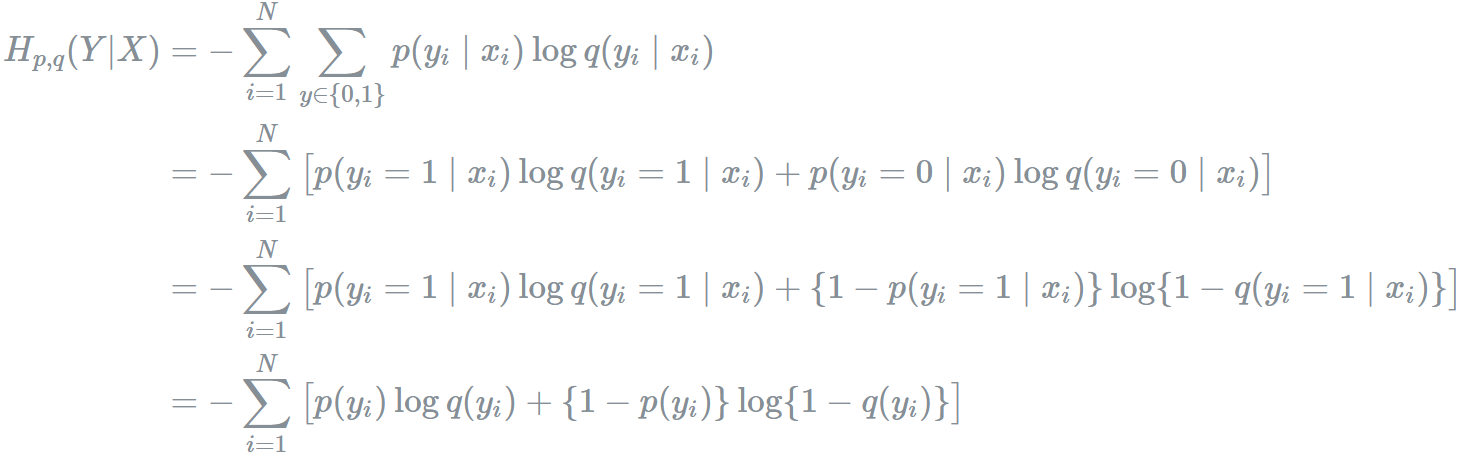
이렇게 Binary cross entropy loss는 Sigmoid activation 뒤에 Cross-Entropy loss를 붙인 형태로 주로 사용하기 때문에 sigmoid cross entropy loss라고도 이야기를 한다.
하지만 이러한 BCE loss function을 discriminator의 object function으로 사용하게 되면 학습이 잘되는것 같지만 사실은 문제가 발생한다.
어떤 문제일까?
바로 Vanishing gradient 문제이다.
왜 그런 문제가 나타나는지 논문에 첨부되어있는 이미지를 통해 살펴보자.
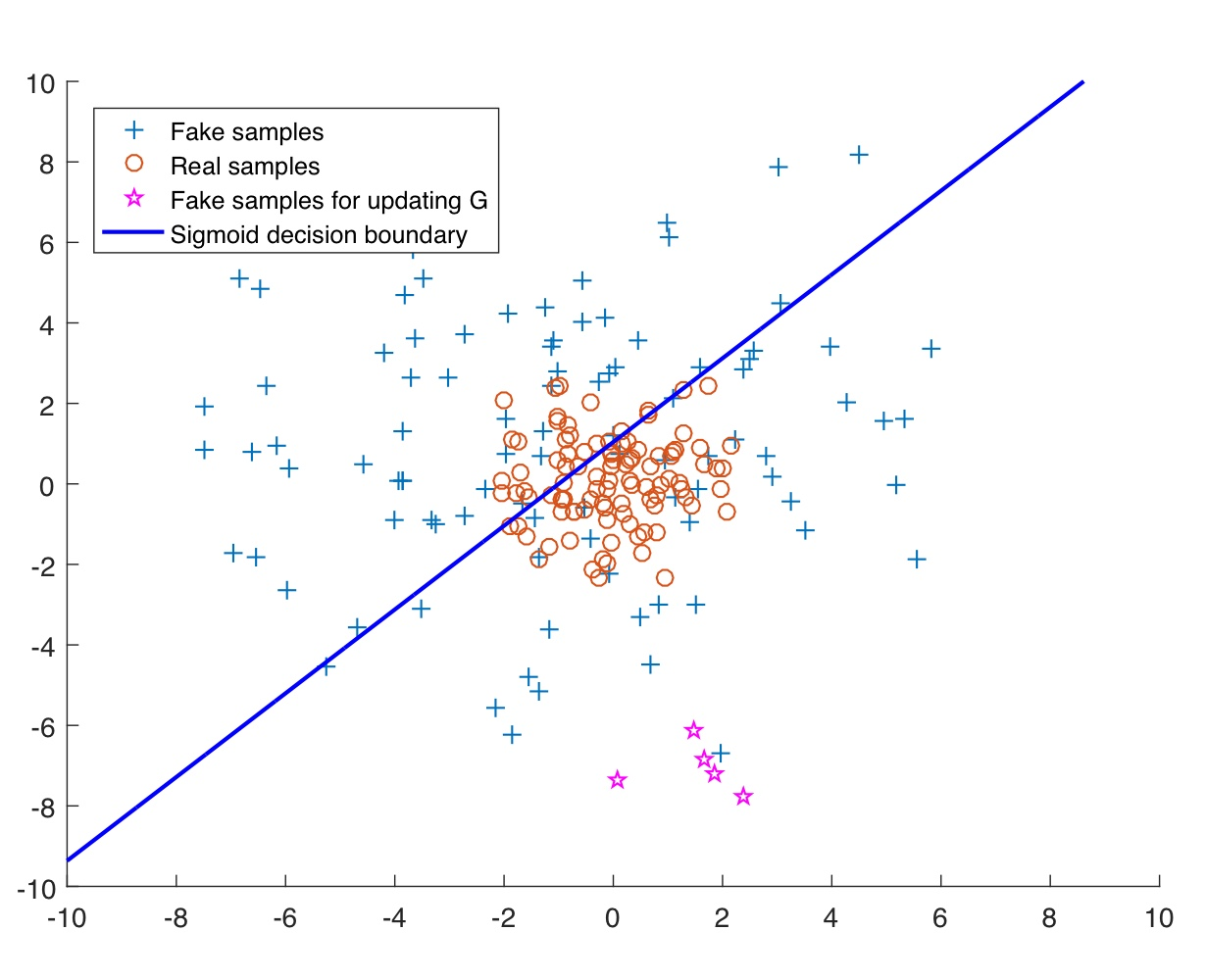
위의 그래프에서 파란색 선이 바로 sigmoid cross entropy loss function의 decision boundary이다.
이 decision boundary는 파란색 선의 아래쪽에 있는 데이터들을 real data로, 위쪽에 있는 데이터들을 fake data로 판단한다. 그리고 가운데 모여있는 빨간색 동그라미들이 실제 real data이고 우리는 generator가 만들어낸 저 +로 표시된 파란색 fake data들을 real data에 가깝게 위치시키고 싶다!
하지만 아래의 분홍색 별 데이터들을 한번 살펴보자. 이들은 fake sample들이지만 boundary 아래쪽에 있기 때문에 판별기는 기준에 따라 저 데이터들을 '진짜'라고 인식한다. 이 데이터들은 이미 진짜로 판단되었기 때문에 Discriminator를 속이는 임무를 완수한 것으로 간주되고, 따라서 더 이상 generator 업데이트에 도움을 주지 않는다.
이렇게 저 별들은 실제로는 real data와 거리가 굉장히 멀지만, 그저 boundary 아래쪽에 있다는 이유로 더이상 업데이트에 도움이 되지 않는 이러한 문제가 발생하게 되고 이 문제를 바로 vanishing gradient문제라고 한다.
그렇기 때문에 우리는 이 vanishing gradient문제를 해결하기 위해 저 별 데이터들을 조금더 real data분포에 가깝게 끌어올 필요가 있고, 이때 LSGAN이 제안하는 것이 바로 binary cross entropy loss대신 decision boundary에서 멀리있는 sample들에게 penalty를 줄 수 있는 Least square loss를 사용하자는 것이다.
Least square loss
아마 least squar error에 대한 개념은 많이 들어보았을 것이기 때문에 간단히 내용만 복기하고 넘어가자.
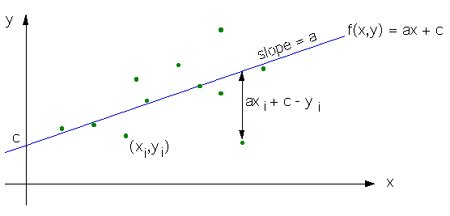
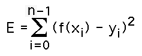
이렇게 어떤 real 값이있고 predict값인 fake 값이 있을 때 그 둘의 차이(거리)를 제곱한 것이 바로 Least square error였다.
즉 , least square는 가짜 데이터들을 거리를 측정한 뒤 그 거리를 낮추는 방향으로 학습을 진행하는 것이다.
바로 이 Least square를 사용했을 때는 GAN에 어떤 변화가 일어나는지 마찬가지로 그래프를 통해 살펴보자.
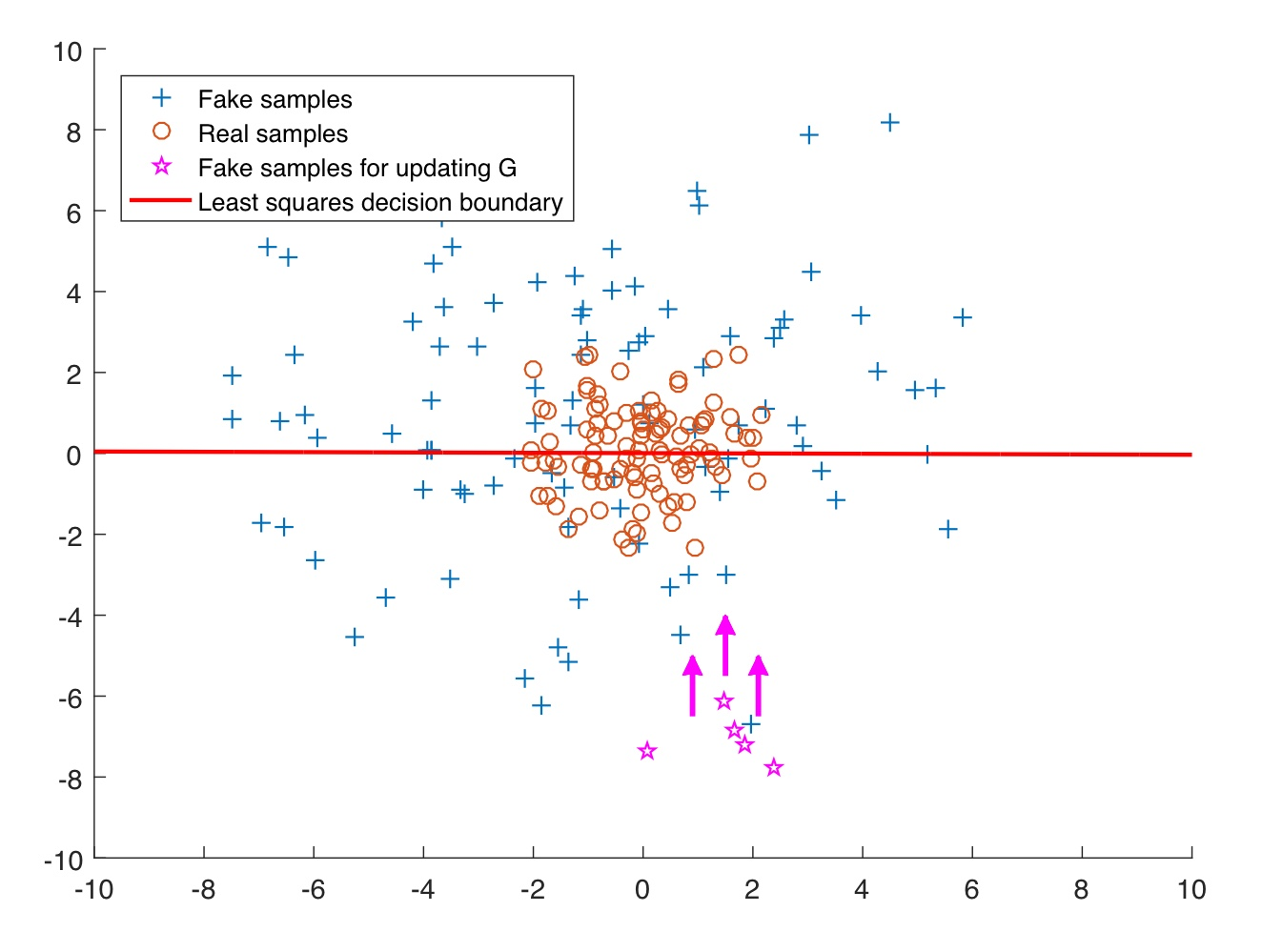
이번에는 빨간색이 바로 Least sqare decision boundary가 된다. 하지만 이때는 least square를 사용했기 때문에 boundary에서 멀리 떨어져있을수록 패널티를 주게된다. 따라서 패널티를 줄이기 위해서 손실함수를 보고 최적화기가 점점 더 결정경계에 가깝게 데이터를 옮김으로써 결국엔 좀더 좋은 real한 데이터 분포에 더 가까울 수 있는 GAN이 되는 것이다.
이렇게 데이터들을 좀더 real한 데이터 분포에 가깝게 위치시키는 것 이외에 LSGAN의 장점이 한가지 더있다.
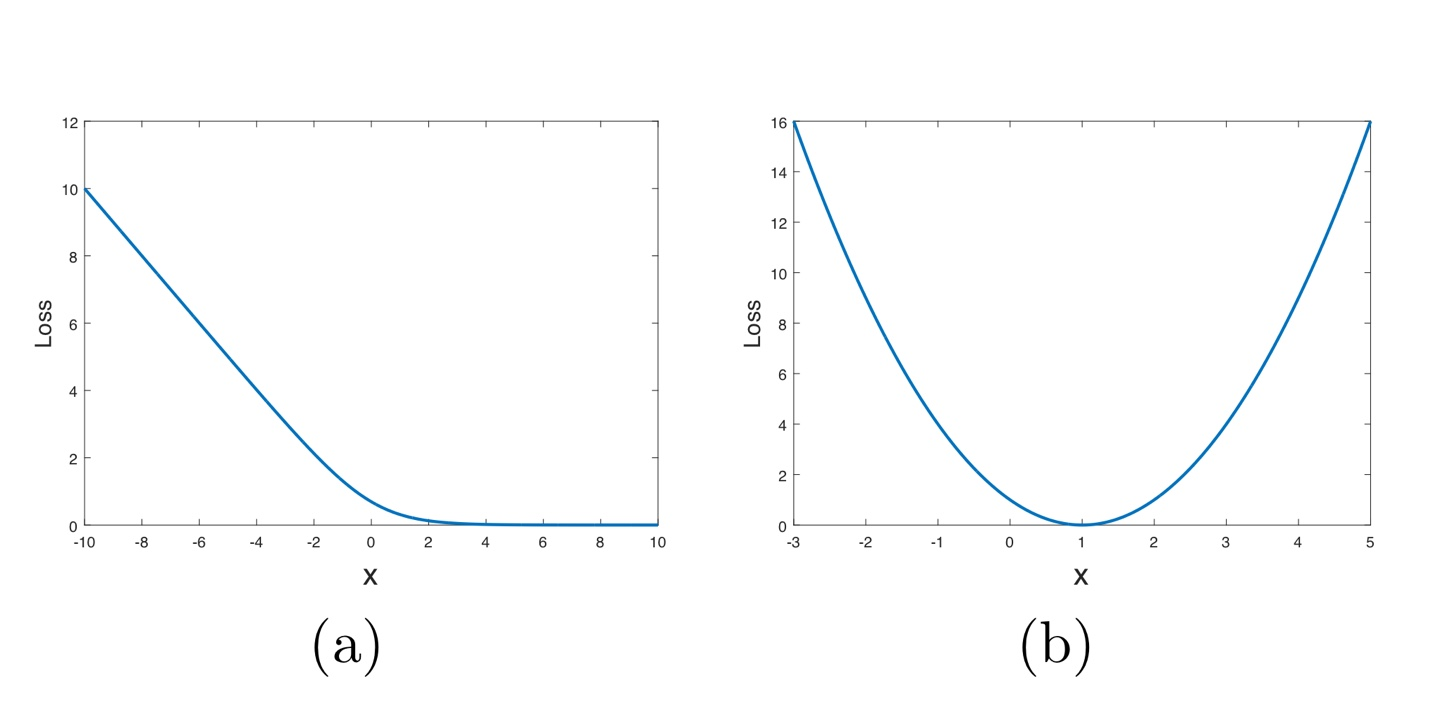
위의 그래프는 sigmoid cross entropy와 least squares loss function을 나타낸 것인데, 그림에서도 볼 수 있듯이 x값에 따라 saturate될 수 있는(weight 업데이트가 멈추는 현상) sigmoid cross entropy loss function과는 달리 least square loss function이 오직 한 점에서만 최소값을 가지기 떄문에 LSGAN이 좀 더 안정적인 학습이 가능하다는 것이다.
이렇게 위의 아이디어를 기존의 GAN과 비교해서 간단하게 수식으로 정리해보면 다음과 같다.
GAN
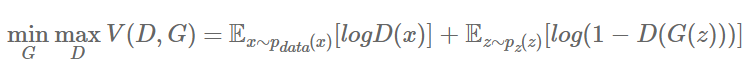
LSGAN
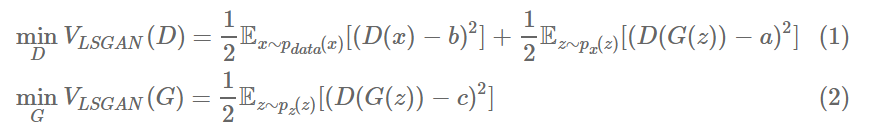
이렇게 LSGAN에서는 식이 약간만 변화를 하게 되어서 a가 fake label, b가 real label, 그리고 c가 G 입장에서 D가 진짜라 믿게 하고자하는 fakes를 의미한다.
Relation to f-divergence
LSGAN 논문에서는 f-divergence와의 관계에 대해서도 한 챕터를 다루고 있다.
결론부터 말하자면 LSGAN이 푸는 문제에 작은 조건을 추가하면 LSGAN 방식이 결국 Pearson x^2 divergence를 최소화하는 것과 같은 것이라는 것이다.
무슨말인지 식을 천천히 따라가보자.
먼저 위에서 언급했듯이 LSGAN에서 우리가 최적화해야할 식은 바로
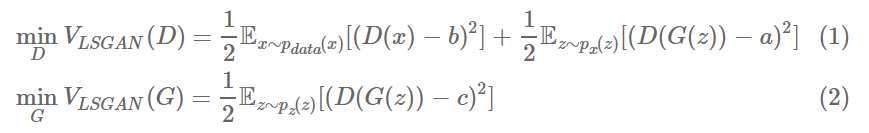
이 식이었다. 이때 이 식을 조금 변형해서 term을 하나 추가해준다.
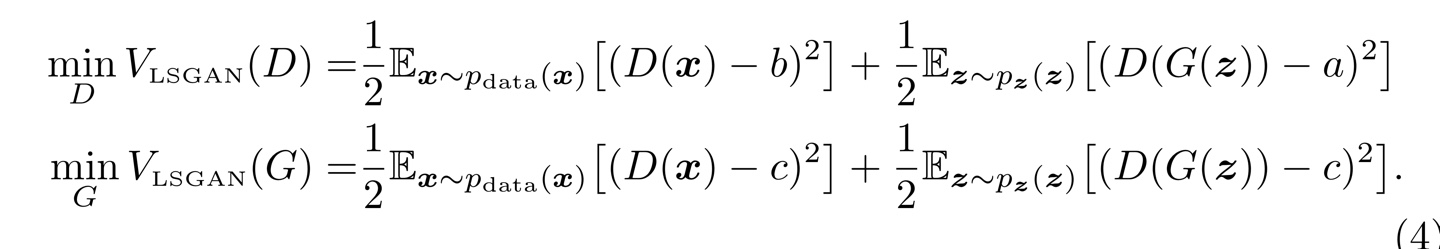
이때 추가된 term은 minV(G)에서 Ex~pdata(x)[(D(x)-c)^2] 부분인데, 이 term에는 어차피 G의 파라미터가 들어가있지 않기 때문에 optimal value에는 영향을 주지 않는다.
이때 G가 고정되었을 때의 optimal D값을 먼저 구해보면 다음과 같다.

증명과정은 GAN과 동일하지만 한번더 식으로 정리해보았다.
어쨌든!! 이제 G가 given일때의 optimal D값을 구했다.
다음은 위에서 구한 D값이 주어졌을 때 generator의 optimal G값을 구해보자!
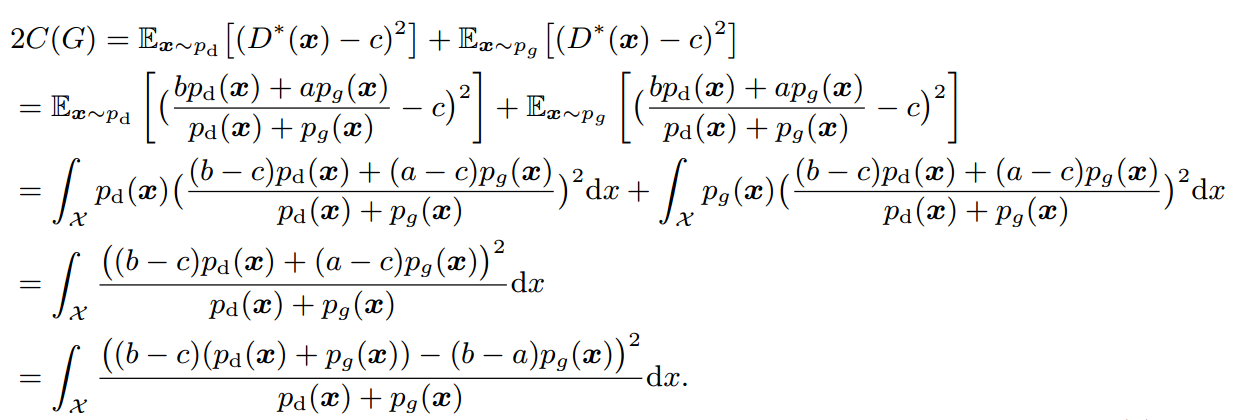
이식은 논문에 제시되어있어서 가져왔다. 식은 어렵지 않고 그냥 계산에 가깝기 때문에 읽어보면 이해할 수 있다.
이렇게 계산되어진 식에 논문에서는 b-c=1, b-a=2라는 조건을 주게 되는데 그렇게 되면 최종식이 다음과 같이 변형될 수 있다.
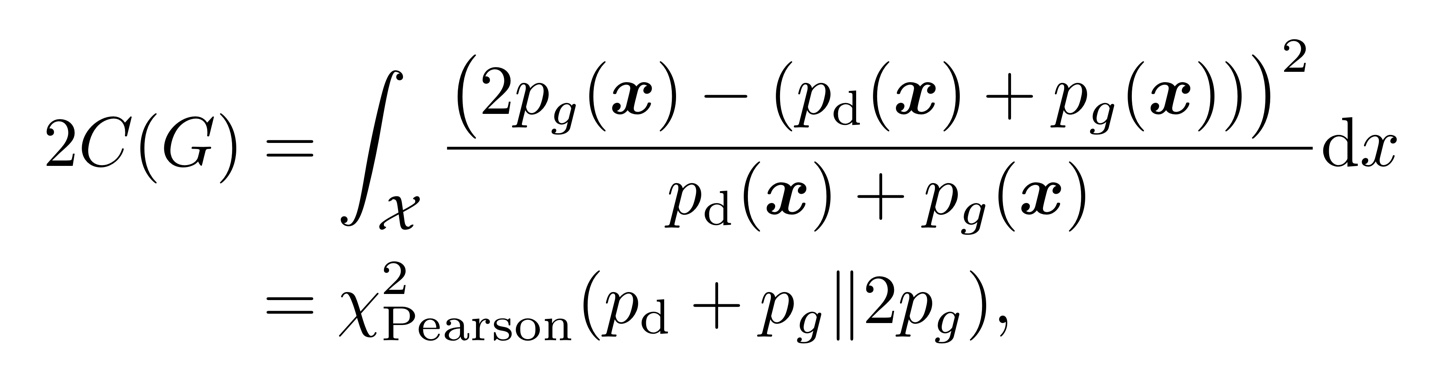
여기서 X^2 Pearson은 Pearson X^2 divergence를 의미한다.
즉! a,b,c가 위의 조건을 만족할 때, LSGAN이 하는 일은 Pg + Pd와 2Pg 사이의 Pearson X^2 divergence를 최소화하는 것과 같은 말이라는 것이다. 따라서 pg=pd일 때 즉, generator가 만들어 내는 sample의 distribution이 data distribution과 같을 때 divergence가 최소가 되어 0이므로 궁극적으로 원래 GAN 가고자 하는 방향과 비슷하다는 것을 보여준다.
f-GAN 논문에서 이야기 하고자 했던 부분 역시도 결국의 JSD 대신 f라는 임의의 divergence로 바꿔도 결국에 GAN과 비슷한 일을 할 수 있다는 것을 보여준 것이기 때문에 LSGAN도 같은 맥락에서 볼 수 있다고 주장하는 것이다.
(사실 f-GAN논문은 아직 안읽어봤지만,, 맥락상으로 그냥 이해하고 넘어갔다,,)
여기서 재밌는 점은 a,b,c가 꼭 저 조건을 따르지 않는 경우에도 딱히 성능이 떨어지지는 않았다는 점이다.
Experiments

마지막은 역시 실험결과를 보여주고 있다. 위의 그림은 DCGAN과 LSGAN, EBGAN을 비교하고 있고, 네트워크 구조는 거의 동일하게 하고 끝의 loss function만 다르게 하였다고 한다. 결과를 살펴보면 LSGAN의 결과가 훨씬 선명하고 진짜같은 이미지를 만들어 냈다는 것을 확인할 수 있다.

다음은 안정성에 대한 실험을 위해서 Batch Normalization의 유무에 따른 결과를 비교해준다.
(a)와 (b)가 Generator에 BN이 없고 Adam을 사용한 경우이고 (c)와 (d)가 Generator와 Discriminator 모두 BN이 없고 RMSProp를 사용한 경우에 대한 결과인데, 그림을 살펴보면 LSGAN이 mode collapse현상(자세한 설명은 여기참고)이 일어나지 않고다양한 이미지를 생성해낸 것을 확인할 수 있다.
이렇게 이번에는 LSGAN에 대해서 정리를 해보았다. 생각보다 간단한 아이디어이지만, 결과를 살펴보면 아주 좋은 것을 확인할 수 있어서 굉장히 흥미롭게 다가왔다! 논문을 읽으면 읽을수록 앞으로 읽게될 논문들이 아주 기대가 된다 :)
<참고자료>
초짜 대학원생의 입장에서 이해하는 LSGAN : jaejunyoo.blogspot.com/2017/04/lsgan-2.html
간단하지만 효과적인 LSGAN과 ACGAN : youtu.be/bqXFcRIhf0I



